Naive Bayes Classifier with Kernel Density Estimation
import pandas as pd
import matplotlib as mpl
import numpy as np
from numpy import mean
from numpy import std
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import LeaveOneOut
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
The Data
To test the classifier, we will use a dataset that contains the season statistics of 275 NBA rookies between 2016 and 1980, and whether or not that player lasted five years or more in the league. The labeled data comes from data world. To add one more feature to the dataset (player efficiency rating), we import another dataset that contains this information.
df = pd.read_csv('NBA.csv') # Import main dataset with labels
df = df.drop(index=29).reset_index(drop=True) # Charles Smith had repeat stats, drop one of his entries
df2 = pd.read_excel('NBA Rookies by Year.xlsx') # Import dataset with player efficiency column
df2 = df2[['Name','EFF','MIN']] # Remove all columns besides player name, efficiency, and minutes per game
df.rename(columns={"name": "Name","min":"MIN"},inplace=True) # Rename columns to use as join keys
df.head()
| X1 | Name | gp | MIN | pts | fgm | fga | fg | 3p_made | 3pa | ... | ft | oreb | dreb | reb | ast | stl | blk | tov | target_5yrs | probability_predictions | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8 | Duane Cooper | 65 | 9.9 | 2.4 | 1.0 | 2.4 | 39.2 | 0.1 | 0.5 | ... | 71.4 | 0.2 | 0.6 | 0.8 | 2.3 | 0.3 | 0.0 | 1.1 | 0 | 0.525373 |
| 1 | 9 | Dave Johnson | 42 | 8.5 | 3.7 | 1.4 | 3.5 | 38.3 | 0.1 | 0.3 | ... | 67.8 | 0.4 | 0.7 | 1.1 | 0.3 | 0.2 | 0.0 | 0.7 | 0 | 0.343556 |
| 2 | 14 | Elmore Spencer | 44 | 6.4 | 2.4 | 1.0 | 1.9 | 53.7 | 0.0 | 0.0 | ... | 50.0 | 0.4 | 1.0 | 1.4 | 0.2 | 0.2 | 0.4 | 0.6 | 1 | 0.385416 |
| 3 | 18 | Larry Johnson | 82 | 37.2 | 19.2 | 7.5 | 15.3 | 49.0 | 0.1 | 0.3 | ... | 82.9 | 3.9 | 7.0 | 11.0 | 3.6 | 1.0 | 0.6 | 1.9 | 0 | 0.990362 |
| 4 | 24 | Mitch McGary | 32 | 15.2 | 6.3 | 2.8 | 5.2 | 53.3 | 0.0 | 0.1 | ... | 62.5 | 1.7 | 3.5 | 5.2 | 0.4 | 0.5 | 0.5 | 1.0 | 0 | 0.439311 |
5 rows × 23 columns
There are repeat names in this dataset such as Mark Davis, Charles Smith, Michael Anderson, and Michael Smith. To deal with these repeat names and ensure correct merging, we will join on two keys, name and minutes played per game
df = df2.merge(df,how = 'inner',on=['Name','MIN'])
df = df.drop(columns = ['Name','X1','probability_predictions']) # Drop non-feature columns
Check for missing values in all columns.
df.isnull().values.any()
False
Visualize the distribution of each feature
Even though Naive Bayes can be used with features that do not adhere to a Gaussian distribution, it is nonetheless interesting to see what distributions represent each feature.
fig = plt.figure(figsize=(15,10))
fig.subplots_adjust(hspace=0.4, wspace=0.4)
fig.supylabel('Number of Rookies',fontsize=20)
for i in range(1, 21):
plt.subplot(4, 5, i)
column = df.columns[i-1]
df[column] = pd.to_numeric(df[column])
this = np.array(df[column])
plt.hist(this,bins=19)
plt.title(f"{column}",fontsize=16)
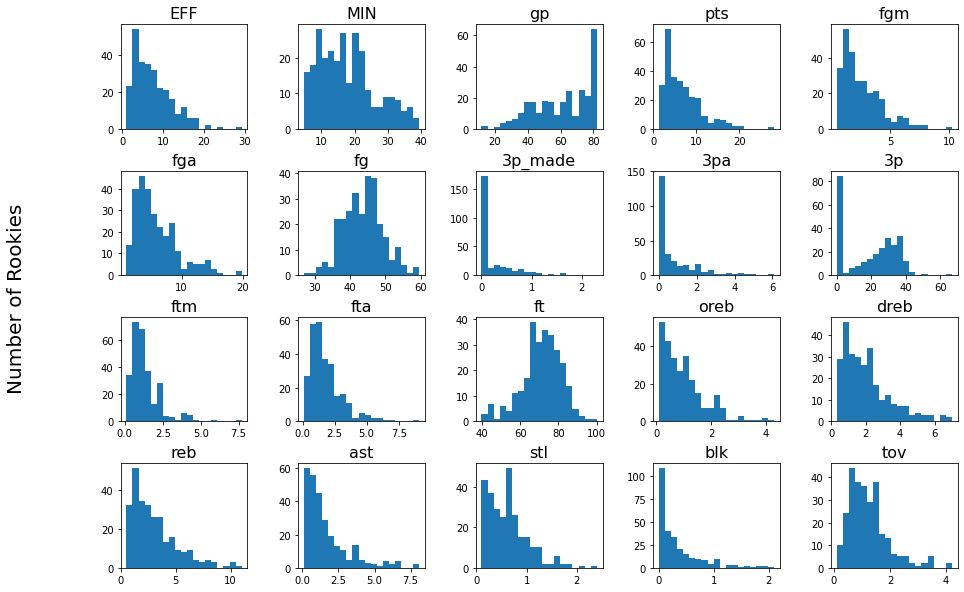
Split the data into training features, evaluation features, training labels, and evaluation labels.
np_random = np.random.RandomState()
rand_unifs = np_random.uniform(0, 1, size = df.shape[0])
division_thresh = np.percentile(rand_unifs, 75)
train_indicator = rand_unifs < division_thresh
eval_indicator = rand_unifs >= division_thresh
train_df = df[train_indicator].reset_index(drop=True)
train_features = np.array(train_df.loc[:,train_df.columns != 'target_5yrs'])
train_labels = np.array(train_df['target_5yrs'])
eval_df = df[eval_indicator].reset_index(drop=True)
eval_features = np.array(eval_df.loc[:,eval_df.columns != 'target_5yrs'])
eval_labels = np.array(eval_df['target_5yrs'])
Naive Bayes Classifier
The following is a from scratch implementation of the naive Bayes classifier.
Function to calculate the log of the prior probabilities. This will calculate the log of the prior probability of an NBA rookie for two conditions, either lasting at least five years in the NBA or exiting the league before their fifth season.
def log_prior_probability(labels):
size = labels.shape[0]
positive_labels = labels.sum()
negative_labels = size - positive_labels
log_py = np.array([np.log(negative_labels/size),np.log(positive_labels/size)]).reshape(2,1)
return log_py
Function to calculate the mean value for each feature. First column contains means for each feature for rookies that have lasted five years or longer in the NBA. Second column contains mean for each feature for rookies that have not lasted five years in the NBA.
def calculate_mean(features, labels):
featuresdf = pd.DataFrame(features)
positive_feats = featuresdf[labels.astype(bool)].reset_index(drop=True)
negative_feats = featuresdf[~labels.astype(bool)].reset_index(drop=True)
avg_positive = np.array(positive_feats).mean(axis=0).reshape(-1,1)
avg_negative = np.array(negative_feats).mean(axis=0).reshape(-1,1)
return np.hstack((avg_negative,avg_positive))
Function to calculate the standard deviation for each feature under the two conditions.
def calculate_std(features, labels):
featuresdf = pd.DataFrame(features)
positive_feats = featuresdf[labels.astype(bool)].reset_index(drop=True)
negative_feats = featuresdf[~labels.astype(bool)].reset_index(drop=True)
std_positive = np.std(np.array(positive_feats),axis=0).reshape(-1,1)
std_negative = np.std(np.array(negative_feats),axis=0).reshape(-1,1)
return np.hstack((std_negative,std_positive))
Function to calculate the log of the conditional probability. This will return the log of the calculated probability of an NBA rookie fitting into the given condition.
def log_conditional_prob(features, avg, std, prior):
log_arg = (1/(std*(np.sqrt(2*np.pi))))
non_log_arg = -0.5*((features - avg)/std)**2
one_feature = np.log(log_arg) + non_log_arg
sum_probability = np.sum(one_feature, axis = 1)
return sum_probability + prior
Function to wrap prior probabilities together in N x 2 array. The first column is the log of the probability that a player does not last five years in the NBA and the second column is the log of the probability that a player does last five years in the NBA. According to the classifier, the greater of these two numbers determines which condition the player is likely to fit into.
def log_prob(train_features, mean_y, std_y, log_prior):
negative_prob = log_conditional_prob(train_features, mean_y[:,0], std_y[:,0], log_prior[0,:][0]).reshape(-1,1)
positive_prob = log_conditional_prob(train_features, mean_y[:,1], std_y[:,1], log_prior[1,:][0]).reshape(-1,1)
return np.hstack((negative_prob,positive_prob))
Naive Bayes classifier class.
class NBClassifier():
def __init__(self, train_features, train_labels):
self.train_features = train_features
self.train_labels = train_labels
self.log_py = log_prior_probability(train_labels)
self.mu_y = self.get_cc_means()
self.sigma_y = self.get_cc_std()
def get_cc_means(self):
mu_y = calculate_mean(self.train_features, self.train_labels)
return mu_y
def get_cc_std(self):
sigma_y = calculate_std(self.train_features, self.train_labels)
return sigma_y
def predict(self, features):
log_p_x_y = log_prob(features, self.mu_y, self.sigma_y, self.log_py)
return log_p_x_y.argmax(axis=1)
Classifier Training and Evaluation
Train and evaluate NB classifier.
nba_classifier = NBClassifier(train_features, train_labels)
train_pred = nba_classifier.predict(train_features)
eval_pred = nba_classifier.predict(eval_features)
def readout(train_pred,eval_pred,train_labels,eval_labels):
train_acc = (train_pred==train_labels).mean()
eval_acc = (eval_pred==eval_labels).mean()
print(f'Training accuracy : {train_acc:.10f}')
print(f'Testing accuracy: {eval_acc:.10f}')
Evaluating the classifier.
readout(train_pred,eval_pred,train_labels,eval_labels)
Training accuracy : 0.5776699029
Testing accuracy: 0.6811594203
Check to see if our implementation matches the naive Bayes classifier from the sklearn library.
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB().fit(train_features, train_labels)
train_sk = gnb.predict(train_features)
eval_sk = gnb.predict(eval_features)
readout(train_sk,eval_sk,train_labels,eval_labels)
Training accuracy : 0.5776699029
Testing accuracy: 0.6811594203
Good, the results from our implementation match the results from the stock algorithm from sklearn.
Cross Validation
The above results represent the classifier accuracy for only one train-test split of the data. To better understand how the naive Bayes classifier performs with the data, we can use leave one out cross validation. This will show us the accuracy of the NB classifier when it acts on data that was not used to train it.
def leave_one_out_cv(df, classifier, stock = False):
cv_array = np.array(df)
X = cv_array[:,0:-1]
y = cv_array[:,-1]
y_true, y_pred, x_vals = np.zeros(df.shape[0]), np.zeros(df.shape[0]), np.zeros(df.shape[0])
for train_ix, test_ix in LeaveOneOut().split(X):
X_train, X_test = X[train_ix, :], X[test_ix, :]
y_train, y_test = y[train_ix], y[test_ix]
if stock == False:
model = classifier(X_train, y_train)
else:
model = classifier.fit(X_train, y_train)
yhat = model.predict(X_test)
y_true[test_ix[0]] = y_test[0]
y_pred[test_ix[0]] = yhat[0]
train_predictions = model.predict(X_train)
train_acc = (train_predictions==y_train).mean()
x_vals[test_ix[0]] = train_acc
acc = accuracy_score(y_true, y_pred)
train_acc = np.mean(np.array(x_vals))
print(f'Training accuracy: {train_acc:.10f}')
print(f'Testing accuracy: {acc:.10f}')
leave_one_out_cv(df,NBClassifier)
Training accuracy: 0.5973855342
Testing accuracy: 0.5963636364
Naive Bayes with Kernel Density Estimation
A Gaussian naive Bayes classifier assumes that each feature in the dataset adheres to a normal distribution. From our visualization of the feature distributions, we can tell that this is not true of our dataset. Although naive Bayes classifiers can still be used in such situations, it stands to reason that if we used non-Gaussian probability density functions to model each feature’s data, we could improve the performance of the classifier. To make such a classifier and build improved probability density functions, we will utilize kernel density estimation. As an illustration of this, the following image shows the probability density distribution for each feature.
fig = plt.figure(figsize=(15,10))
fig.subplots_adjust(hspace=0.4, wspace=0.3)
fig.supylabel('Probability',fontsize=20)
for i in range(1, 21):
plt.subplot(4, 5, i)
column = df.columns[i-1]
x_d = np.linspace(-10, 110, 2000)
x = np.array(df[column]).reshape(-1, 1)
kde = KernelDensity(bandwidth=2.25701971963392, kernel='gaussian')
kde.fit(x)
logprob = kde.score_samples(x_d[:, None])
plt.yticks(fontsize=8)
plt.xticks(fontsize=8)
plt.fill_between(x_d, np.exp(logprob), alpha=0.5)
plt.xlim((x.min()-7,x.max()+5))
plt.ylim(-0.02, np.exp(logprob).max()+0.01)
plt.title(f"{column}",fontsize=16)
plt.plot(x, np.full_like(x, -0.01), '|k', markeredgewidth=0.1)
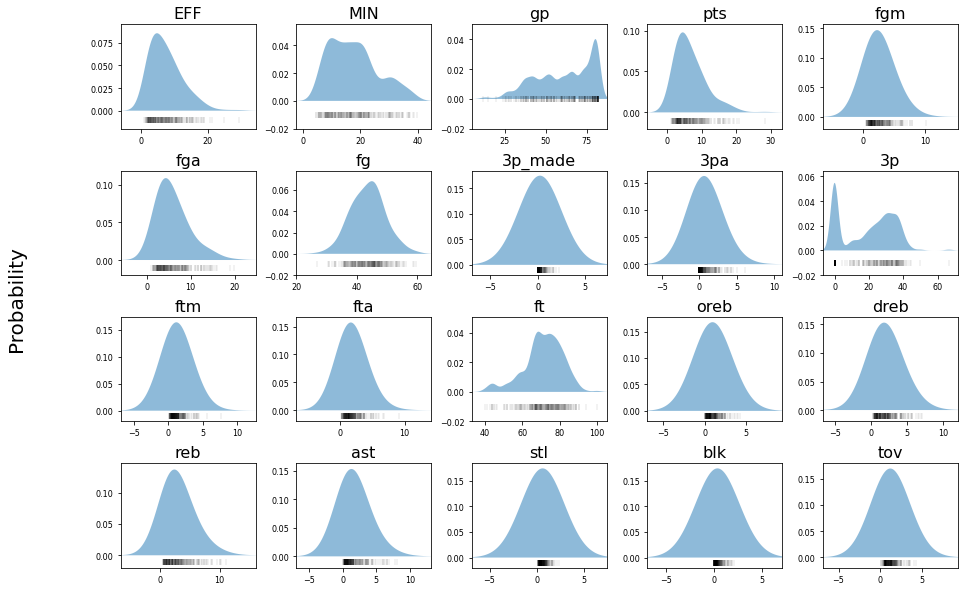
To get the best performance out of the improved classifier, we need to tune the bandwidth hyperparameter for the Kernel Density Estimation with our specific dataset. We can do this using the GridSearchCV function from sklearn.
from sklearn.model_selection import GridSearchCV
bandwidths = 10 ** np.linspace(-1, 1, 100)
grid = GridSearchCV(KernelDensity(kernel='gaussian'),
{'bandwidth': bandwidths})
grid.fit(df)
grid.best_params_
{'bandwidth': 2.25701971963392}
Rather than calculating the mean and standard deviation of each feature (under each of the two conditions) to define the Gaussian distributions, we instead pass the features (under each of the two conditions) to the kernel density estimation function in order to define a probability density function that more accurately represents the data.
def create_models(training_fts,train_labels):
featuresdf = pd.DataFrame(training_fts)
pos_fts = np.array(featuresdf[train_labels.astype(bool)].reset_index(drop=True))
neg_fts = np.array(featuresdf[~train_labels.astype(bool)].reset_index(drop=True))
pos_models = np.array([KernelDensity(bandwidth = 0.12618568830660204).fit(pos_fts[:,i].reshape(-1,1)) for i in range(training_fts.shape[1])])
neg_models = np.array([KernelDensity(bandwidth = 0.12618568830660204).fit(neg_fts[:,i].reshape(-1,1)) for i in range(training_fts.shape[1])])
return np.hstack((neg_models.reshape(-1,1),pos_models.reshape(-1,1)))
def sum_log_likelihood(features, models, prior):
logprobs = np.zeros(features.shape)
for i in range(features.shape[0]):
for j in range(features.shape[1]):
logprobs[i,j] = models[j].score(features[i,j].reshape(-1,1))
return np.sum(logprobs,axis=1) + prior
def log_probability(features,models,log_py):
neg_prediction = sum_log_likelihood(features,models[:,0], log_py[0,:][0]).reshape(-1,1)
pos_prediction = sum_log_likelihood(features,models[:,1], log_py[1,:][0]).reshape(-1,1)
return np.hstack((neg_prediction,pos_prediction))
Class for naive Bayes classifier with kernel density estimation.
class KDEClassifier():
def __init__(self, train_features, train_labels):
self.train_features = train_features
self.train_labels = train_labels
self.log_py = log_prior_probability(train_labels)
self.models = create_models(self.train_features, self.train_labels)
def predict(self, features):
predictions = log_probability(features, self.models, self.log_py)
return predictions.argmax(axis=1)
KDE Classifier Training and Evaluation
kde_classifier = KDEClassifier(train_features, train_labels)
train_pred = kde_classifier.predict(train_features)
eval_pred = kde_classifier.predict(eval_features)
readout(train_pred,eval_pred,train_labels,eval_labels)
Training accuracy : 0.9174757282
Testing accuracy: 0.7246376812
Cross Validation of KDE classifier
leave_one_out_cv(df,KDEClassifier)
Training accuracy: 0.8849236894
Testing accuracy: 0.6254545455
Compared to the stock naive Bayes classifier, our improved KDE naive Bayes classifier performed about 3% better. Not incredible, but a notable improvement over the base model. To see how other classifiers perform on this dataset, we can use several prebuilt classifiers from the sklearn library. We will also perform leave one out cross validation to preclude any aberrant results.
Comparison to other stock sklearn classifiers
leave_one_out_cv(df,DecisionTreeClassifier(),stock=True)
Training accuracy: 1.0000000000
Testing accuracy: 0.6400000000
leave_one_out_cv(df,RandomForestClassifier(n_estimators=300),stock=True)
Training accuracy: 1.0000000000
Testing accuracy: 0.6690909091
leave_one_out_cv(df,KNeighborsClassifier(n_neighbors=20),stock=True)
Training accuracy: 0.7340544127
Testing accuracy: 0.7090909091
leave_one_out_cv(df,LogisticRegression(penalty = 'none',max_iter=10000),stock=True)
Training accuracy: 0.7446449900
Testing accuracy: 0.6945454545
Clearly, the naive Bayes classifier and the KDE naive Bayes classifier are not the best options when it comes to binary classification. Nonetheless, this dataset does not play to the strongsuits of naive Bayes classifiers. For example, the features in our dataset are not independent. That is, usually a stellar player will have stellar stats in all categories. Naive Bayes can actually perform admirably in situations where features are indeed independent (not just assumed to be independent) and may also perform well with categorical features rather than continuous features.
